CharBug2

Introduction

Recently, I had the opportunity to participate in the CharBug2 programming contest held in Isfahan, where I’m from. It was an exciting and challenging experience that tested our problem-solving skills and algorithmic thinking. In this post, I’ll share my experience and walk you through one of the problems we solved.

Contest Overview

The contest featured 12 challenging problems covering various topics in competitive programming, including algorithms, data structures, and mathematical concepts. Our team, “shokolat”, managed to solve 3 out of 12 problems during the competition time.

While we didn’t solve all the problems, the experience was incredibly valuable. Each problem required careful analysis, efficient algorithm design, and proper implementation. Let me share one of the problems we successfully solved.

Problem A: Finding the Next Perfect Square

Before diving into the solution, here’s our team’s position on the scoreboard:

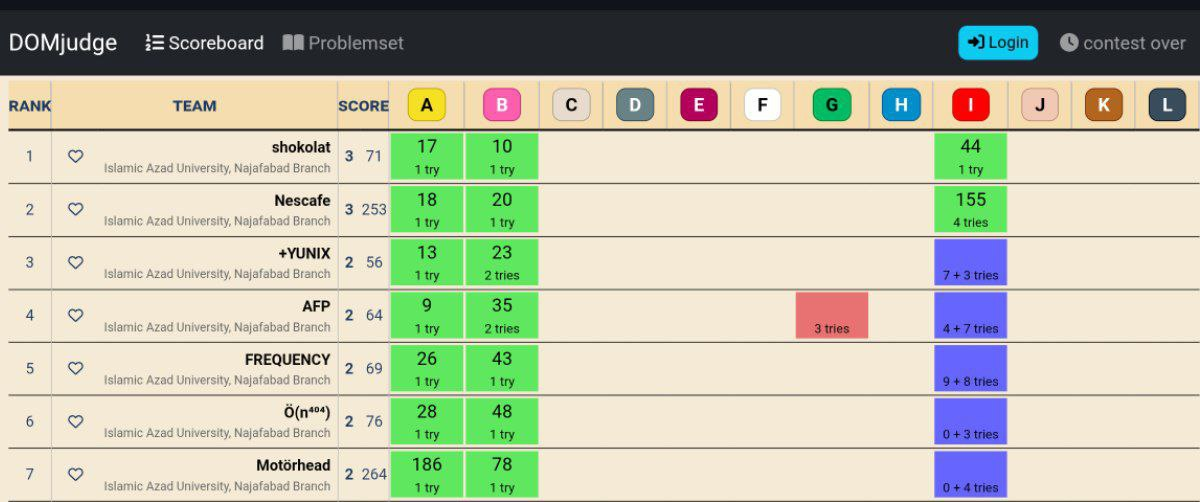
Now, let’s solve Problem A together. Here’s the problem statement:

Problem Analysis

The problem asks us to find the minimum number we need to add to a given number n to make it a perfect square.

A perfect square is a number that can be expressed as the product of an integer with itself. For example:

• 25 = 5 × 5, so 25 is a perfect square
• 16 = 4 × 4, so 16 is a perfect square
• 10 is not a perfect square

If the input number is already a perfect square, we should return 0. For instance, if n = 25, we don’t need to add anything, so the answer is 0.

Solution Approach

A straightforward approach is to:

1. Start with the given number n
2. Check if it’s already a perfect square
3. If not, increment n and check again
4. Count how many increments we need until we find a perfect square

In Python, we can check if a number is a perfect square by calculating its square root. If the square root is an integer, then the number is a perfect square. We can do this by checking if n ** 0.5 equals int(n ** 0.5).

Implementation

Here’s the solution we implemented:

for _ in range(int(input())):
    n = int(input())
    ans = 0
    while n ** 0.5 != int(n ** 0.5):
        n += 1
        ans += 1
    print(ans)

Explanation

1. We read the number of test cases
2. For each test case, we read the number n
3. We initialize ans to 0 to count the increments
4. We loop while n is not a perfect square (i.e., while n ** 0.5 != int(n ** 0.5))
5. In each iteration, we increment n and ans
6. Once we find a perfect square, we print the answer

Time Complexity

The time complexity of this solution is O(k × m), where k is the number of test cases and m is the maximum number of increments needed. While this approach works for the given constraints, there are more efficient mathematical approaches that could find the next perfect square directly without iteration.

Conclusion

Participating in CharBug2 was a great learning experience. It challenged us to think critically, work efficiently under time pressure, and collaborate as a team. Even though we only solved 3 problems, each one taught us something valuable about problem-solving strategies and algorithm design.

If you’re interested in competitive programming, I highly recommend participating in such contests. They’re excellent opportunities to improve your coding skills, learn new algorithms, and meet other passionate programmers.

Video Recap

Here’s a video recap of the CharBug2 contest in Persian: